为何要抽检5件？Why Sampling 5pcs?

Views: 294

为何要抽检5件？

2007年参观欧洲的某公司的生产线，遇到一个抽样检查的问题，当时是巡检的频率以及抽检的数量和中国同产品的代工厂不一样，从欧洲人的角度看，他们认为代工厂巡检时的检验效率过低，因为除了欧洲当时广泛运用自制的Go/NoGo检具之外，当时我们抽检的数量是10pcs，欧洲人认为比较高，但是代工厂没有人能讲清楚，为什么是那个抽检的数量？当时我和欧洲人聊起这个话题，他们给了我非常逻辑性的抽样概率的解释，虽然当时听得半懂，但是此事让笔者一直记忆尤深。

直到今日，国内的很多工厂在巡检时定义巡检的数量和频率仍然毫无章法，很多时候也就是依照经验。

无独有偶，笔者的团队近期也碰到一个类似的难题。有一个注塑件供应商在提交PPAP时坚持每一穴只检测一个样品，当然他们接受模具里的每一穴都会检测。争议点在于只测一件会不会太少，供应商给出他们的逻辑：
1. 尺寸比较稳定，测一件基本能代表同一穴的样品尺寸。
2. 图纸上标注的产品的尺寸比较多，如果要全部测，并且每一穴多测的话会比较耗时，不能满足客户要求的提交时间。
3. 最终产品品质的风险是由供应商承担，如果客户强制要求多检测，产品的检验和测试费用会增加，供应商不愿意承担这笔费用。

团队经过内部调查，发现以下事实：
1. 的确供应商的价格我们压的比较低。
2. 其他类似的产品的供应商有的每穴测三件，有的测五件。
3. 为了寻求一个标准，大家特意去查阅了PPAP手册里面关于全尺寸测量的要求，发现并没有提及这种情况下的测量数量。PPAP 手册第4版规定如下：

4. 同时又翻阅了相关的本公司制定的产品质量指引，发现也没有任何提及和规定。

这时大家感觉无所适从，认为需要采购的同事去给供应商施压，这种靠供应商卖面子的事情其实谁去做都可以，与技术无关。

首先，从中央极限定理来看，分组样本量>=5时，样本均值近似正态分布；其次多观测几次测量结果有助于减少测量系统的误差。

其次，我们如果从概率的角度来看待这个抽样数量，就会发现这里面有简单的逻辑存在可以供参考。

抽检一件产品，在前提不知道合格率的情况下，产品合格与否属于0-1分布，每件样品合格的概率在50%（不合格的概率也是50%），也就是0.5，随机抽检第二件产品，合格的概率依然是50%，以此类推，抽检任何一件产品，合格的概率均是50%。多次抽取，合格的次数（0，1，2，。。。。。。）按二项分布排列。

如果我们只抽一件产品，合格的概率是50%，也就是说，即便测量结果是合格的，我们能推断这个穴所加工出来的产品的合格概率只有50%。

如果我们抽两件产品，两件合格的概率均是50%，整体合格的概率就是50% * 50%=25%。

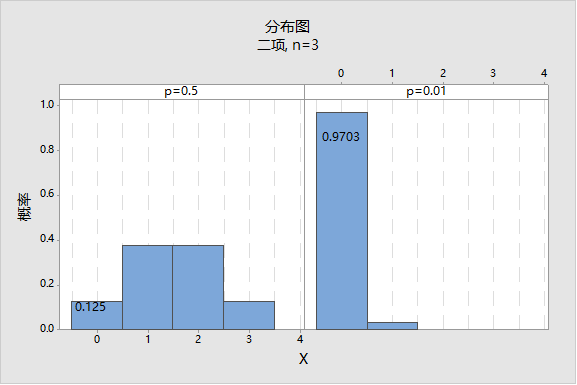
而如果我们抽三件产品，三件合格的概率也是各为50%，整体合格的概率为50% * 50% * 50%=12.5%。

（以上是假设不知道0-1分布中不合格率的情形，如果假设知道不合格水平在1%，这时三件整体合格的概率为（1-0.01）³=0.9703，如此高的概率，笔者愚见抽检3件的意义并不大）

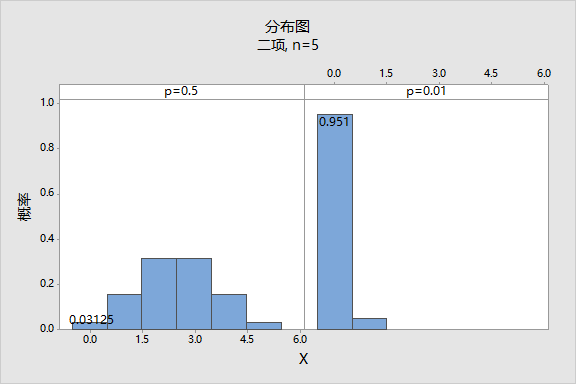
如果我们抽五件产品，整体合格的概率就只有3.125%左右，这么低（小于5%) 的概率下面如果五件都合格，意味着我们比较有信心，这个穴所对应的尺寸会合格。（同理，如果假设不良率为1%，抽检5件全合格的概率为0.951，如此之高也是没有必要抽检5件）

由此，团队认为可以接受12.5% 的风险，从而同意给供应商定义最小的测量数量为3件。回到本文开始的问题，答案也就不言而喻了，笔者猜测这也是为什么大部分公司在巡检时检验5件的原因。

抽检5件可以以较低的风险或者较高的置信度来接收或判断此时的产品是符合要求规格的，下一个问题是如果需要判定不仅符合规格，而且此时过程还稳定，按照预控图的理论，仍然是要连续抽检5件。

同样的思路，假设某产品平均的不良率为5%，而连续抽检2件都发现不合格，也就是两件都不合格的概率为5%*5%=0.25% （远小于5%），如此低的概率下都能都发现，说明此时的不良率远高于5%；同理，假设（x%）^3>5%, 可以计算出x%>36.84%，也就是说连续抽检3件，3件都不合格，这种总概率约在5%的情况都能被发现，说明此时的不良率已经大于36.84%了。

按照离散数据二项分布的理论，概率P(X=x)= * p^x * (1-p) ^(n-x) , x=0,1,…, n. 称为X 服从二项分布，每次实验成功的概率为p, 失败的概率为 （1-p），X 为“n 次独立重复实验中成功的次数”，在样本批小于总批量10%的情形下，超几何分布（无放回抽样）也可用二项分布近似估算，二项分布的均值E（X）=np, 方差var（X）=np(1-p), 标准差σ(X)=。将上面不良率为5%的连续抽检2件不合格的情形代入公式计算，此时P(X=2)= * 5%² * (1-5%) ^(2-2) =0.25%，而平均不良率为E（X）=2*5%=10%，如果是连续抽检3件不合格，同理计算P(X=3)=0.0125%，此时平均不良率E(X)=15%，当然按照统计学理论，如果np>=5或者n(1-p)>=5时，就需要用正态分布作为一个近似估算了。

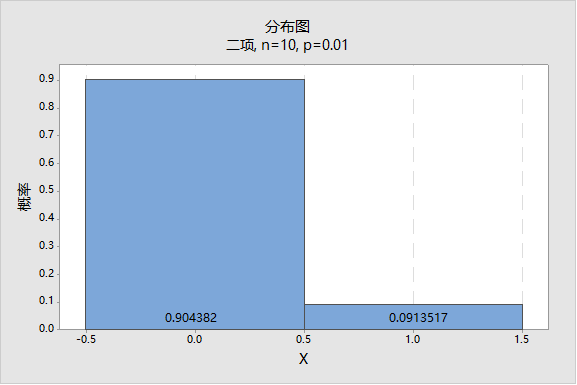
类似的基础统计理论运用还有很多，比如供应商交货1000件，历史平均不良率1%，抽检10件，请问发现1件不合格的概率（机会）有多高？ 答案是9.14%，见如下Minitab 的计算，当然读者也可以套用上面二项分布的公式来计算。

进一步归纳，我们常见的可靠性试验应该重复几个样品的试验？如果检验员进行某种测试和检验，比如拉力强度，或者硬度检验，又应该抽取几个（组）样品进行试验比较可靠？检验的结果第一次不合格（比如电线压接端子的断面分析），员工怀疑是检验操作手法不够准确，是否应该直接做不合格的判定，还是应该另外再测几次比较合理，究竟应该再测几次合格会有比较可靠的判断呢（假设测量系统已经经过确认是合格的）？