Views: 334
首先生产过程有三种状态,要么停机,要么正常生产,要么有异常。停机好理解,那么何为正常生产,何为异常?
所谓正常,是指稳定的状态,也就是统计理论里的稳定受控状态,而异常,也就是非稳定受控状态。在GB/T 17989.1-2020 控制图-第一部分 通用指南里,对过程稳定的判断是 “过程是否在一个仅有随机原因影响的系统内运行,此时过程发生的变异称为固有变异,也称该过程处于‘统计受控状态’”。[1] “如果发现过程并不处于统计受控状态,则称之为失控,此时需要采取干预措施,使过程恢复至统计受控状态。。。。。。“,失控就是所谓的异常。

戴明在其著作《***》里反复强调不要试图去对一个不稳定的过程进行“破坏”,那只会打破现有的不稳定状态而越弄越乱,不稳定的过程首先需要找到造成不稳定的特殊原因并消除,使其变得稳定,在此基础之上在进行系统上的改善才能有助于提升稳定的层级和水平。在《***》里戴明大师举了很多的判别系统是否稳定的例子,笔者借此也来尝试印证于我们日常的生产管控中。
快速反应(Quick Response Quality Control, QRQC,后人也简称为快反)是由90年代的尼桑公司创造的,2002年由法雷奥所采用,在通用汽车GM的管理方法BiQS (Build in Quality System)里也有着重强调。每家公司实施的全过程不可能完全相同,但是重点确都是对异常和重大问题做出快速反应。

Figure 1佛吉亚内部培训资料

在实践中大家如何定义重大问题(Significant issues)和异常(Non-conformities) ?
笔者所在的公司遵循的其中一个是称为X,Y,Z的原则,也就是
- 连续不良小于X件(比如3件)
- 每小时累计不良小于Y件(比如3件)
- 每班次累计不良小于Z件(比如3件)
超过这个数量会被定义为异常,要求启动现场快反会议和措施,如果涉及供应商来料造成的问题则会被记为投诉(如果没超过这个预先定义的值,会被记为PPM 的不良)。那么X,Y,Z的数量限制又是基于何种逻辑制定的呢?笔者无缘去向当初拟定这个标准的前人求教,但是在向执行这个标准的现场人员求证后,经验告诉我这个标准是基于历史的经验得出来的。但是基于戴明博士在《转为为安》中的一些启发,将笔者公司的需要启动反应措施的情形进行了一些梳理,如下:

异常的类型首先被分为关键的少数和传统的大多数的,关键的问题自然发生的概率应该非常低(或者可接受的概率应该非常高),比如说<50PPM (参考FMEA 手册的发生频率度), 如此低的概率下能发生,自然有必要立即展开调查以了解制程发生变异的特殊原因,比如说安全问题。
另外一类则是原因不明确的不良,比如新型的缺陷;经过一段时间的运作,才发现的不良。
除了这些关键的问题,还有一类就是我们常见的品质问题,也就是柏拉图里次要的多数,比如外观问题,修理岗位(可修理的缺陷)发现的普通缺陷,这些更合适定义X,Y,Z的原则。我们以它们历史发生的平均概率0.1%(1000PPM),每小时的平均产出1000PCS,不良按照二项分布来计算上下控制限,也就是计件控制图的控制限:
UCL=np+3√n*p0*(1-p0)=3.998≈4
LCL= np-3√n*p0*(1-p0) 为负数(-1.998),取值0,
也就是说如果生产过程稳定的话,不良数在0到4之间变化是正常的,也就是说我们X和Y取4比较合理。当然这里X可以取比4还小,因为连续4件不良的概率为0.1%*0.1%*0.1%*0.1% = 1.E-12,非常非常小的概率都会发生,自然这种异常是需要采取快反的。对于Y而言,每小时的不良在4件以内无需管理层“逼迫”团队去大费周折寻找所谓的“特殊原因”,如果要追求进一步的改善,按照戴明博士的解释,这是管理层需要从系统上查证并改进的,而不是快反所要解决的问题。
对于定义合适的Z而言,我们假设平均每天的工作时间为10小时,也就是每天的生产量为10,000件,平均不良仍然为0.1%,同样不良按照二项分布来计算上下控制限:
UCL=np+3√n*p0*(1-p0)=19.482≈20
LCL= np-3√n*p0*(1-p0) =0.518≈1,
1件到20件,这是稳定的生产状况下会产生不良的范围,也就是Z的取值范围。如果按照反应控制限Z超过4件就要采取措施的话(笔者产线实际就是采用以每天最多4件为限),只会打乱稳定的生产状态,也就是戴明博士的漏斗实验情形 – 只会加大过程的不稳定性。
控制限计算出的是理论的“异常”限,也就是需要调查“特殊原因”的反应限,而至于停线的触发限X1,Y1,Z1,则更多是基于公司制定的目标值。
除了品质问题,效率的波动和损失也可以用控制限的原理来加以解释,也就是说即便是稳定的生产条件下,单位时间的产出也会因存在波动而构成一个范围,而不是达到目标产出或者节拍产出就是达标,而达不到就是不达标。这如同笔者每日往返家和公司,走同样的线路,也基本上是同样的出发时间,但是几乎做不到到达公司和家的时间是同一个时间点,也就是说驾驶的时间总会在一个范围内波动。很特殊的情况下,比如放长假的前一天,基本上下班后从公司到家的时间就会特别长;相反在放长假期间如果由家到公司的话,则会非常顺利,驾驶时间远比平时通勤时间短。
某公司平均的每小时产量为377件,进而也被列为计划产量,此处可以利用Xbar-R控制限的计算公式来求解上下控制限, 笔者以戴明的经验公式求得:
UCL=n+3√n=377+58=435
LCL=n-3√n=377-58=319
也就是说某小时产量的波动在319-435件之间均是稳定的波动范围,超过58件的波动为异常波动,需要调查原因,以下面的现场统计为例,14:00-15:00间的波动达到87件,而“特殊原因”就是“转机30分钟”,其它时间段的波动则在58以内,属正常的波动,试图对于其它例如单小时的产出波动为13PCS,8PCS,10PCS 等等的调查均是无助甚至有害的。
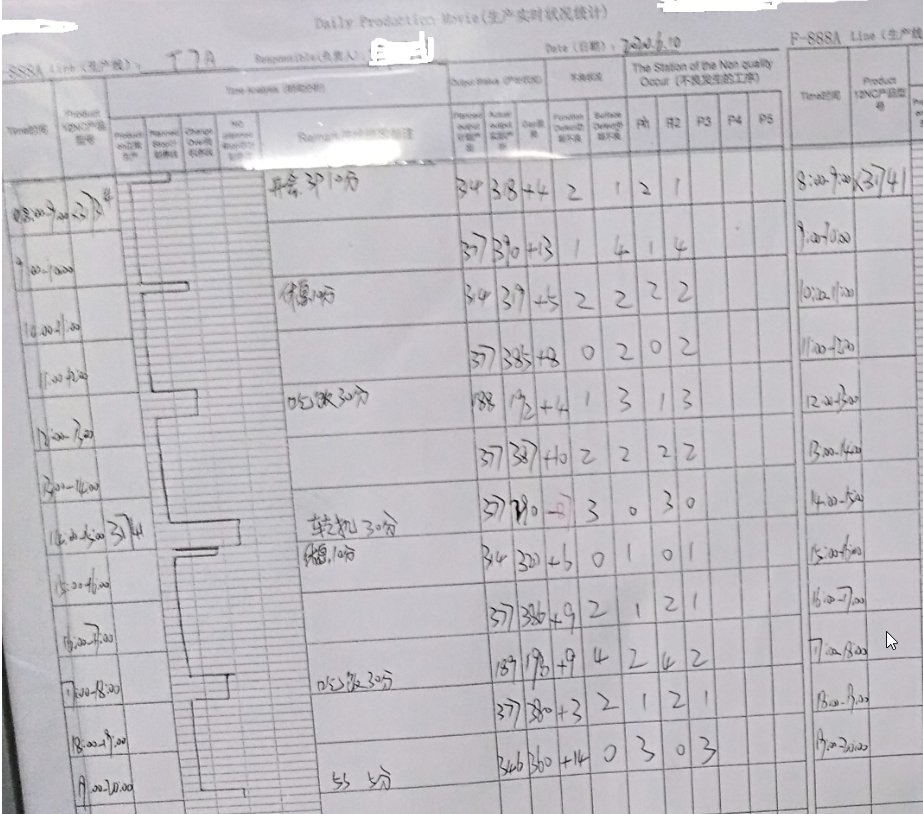
那么如何缩小例子中虽然稳定但是看似+/-15%的波动呢,措施则在于管理层系统的原因调查和系统层面的措施,而不是在于现场人员对“特殊原因”的行动。

Figure 2 GB/T17989.2-2020 常规控制图
举一反三,对于组织和团队目标的设定,通常的做法是基于预算,从上而下依次将总体目标结合平衡积分卡的原则依次展开,但是很多并不符合戴明博士对于合理的稳定性的指导,具体的分析请搜索其他文章。
- GB/T 17989.1-2020 控制图-第一部分 通用指南 ↑
 粤ICP备2022015479号-1 All Rights Reserved © 2017-2023
粤ICP备2022015479号-1 All Rights Reserved © 2017-2023